"I am the Lorax. I speak for the trees. I speak for the trees for they have no tongues."
—Dr. Seuss (The Lorax)
People see winter as a cold and gloomy time in nature. The days are short. Snow blankets the ground. Lakes and ponds freeze, and animals scurry to burrows to wait for spring. The rainbow of red, yellow and orange autumn leaves has been blown away by the wind turning trees into black skeletons that stretch bony fingers of branches into the sky. It seems like nature has disappeared.

But when I went on a winter hiking trip in the Catskill Mountains in New York, I noticed something strange about the shape of the tree branches. I thought trees were a mess of tangled branches, but I saw a pattern in the way the tree branches grew. I took photos of the branches on different types of trees, and the pattern became clearer.
The branches seemed to have a spiral pattern that reached up into the sky. I had a hunch that the trees had a secret to tell about this shape. Investigating this secret led me on an expedition from the Catskill Mountains to the ancient Sanskrit poetry of India; from the 13th-century streets of Pisa, Italy, and a mysterious mathematical formula called the "divine number" to an 18th-century naturalist who saw this mathematical formula in nature; and, finally, to experimenting with the trees in my own backyard.
My investigation asked the question of whether there is a secret formula in tree design and whether the purpose of the spiral pattern is to collect sunlight better. After doing research, I put together test tools, experiments and design models to investigate how trees collect sunlight. At the end of my research project, I put the pieces of this natural puzzle together, and I discovered the answer. But the best part was that I discovered a new way to increase the efficiency of solar panels at collecting sunlight!
My investigation started with trying to understand the spiral pattern. I found the answer with a medieval mathematician and an 18th-century naturalist. In 1209 in Pisa, Leonardo of Pisano, also known as "Fibonacci," used his skills to answer a math puzzle about how fast rabbits could reproduce in pairs over a period of time. While counting his newborn rabbits, Fibonacci came up with a numerical sequence. Fibonacci used patterns in ancient Sanskrit poetry from India to make a sequence of numbers starting with zero (0) and one (1). Fibonacci added the last two numbers in the series together, and the sum became the next number in the sequence. The number sequence started to look like this: 1, 1, 2, 3, 5, 8, 13, 21, 34... . The number pattern had the formula Fn = Fn-1 + Fn-2 and became the Fibonacci sequence. But it seemed to have mystical powers! When the numbers in the sequence were put in ratios, the value of the ratio was the same as another number, φ, or "phi," which has a value of 1.618. The number "phi" is nicknamed the "divine number" (Posamentier). Scientists and naturalists have discovered the Fibonacci sequence appearing in many forms in nature, such as the shape of nautilus shells, the seeds of sunflowers, falcon flight patterns and galaxies flying through space. What's more mysterious is that the "divine" number equals your height divided by the height of your torso, and even weirder, the ratio of female bees to male bees in a typical hive! (Livio)
The spiral on trees showing the Fibonacci Sequence

Aidan studied leaf arrangments

Aidan measuring the spiral pattern
In 1754, a naturalist named Charles Bonnet observed that plants sprout branches and leaves in a pattern, called phyllotaxis. Bonnet saw that tree branches and leaves had a mathematical spiral pattern that could be shown as a fraction. The amazing thing is that the mathematical fractions were the same numbers as the Fibonacci sequence! On the oak tree, the Fibonacci fraction is 2/5, which means that the spiral takes five branches to spiral two times around the trunk to complete one pattern. Other trees with the Fibonacci leaf arrangement are the elm tree (1/2); the beech (1/3); the willow (3/8) and the almond tree (5/13) (Livio, Adler).
I now had my first piece of the puzzle but it did not answer the question, Why do trees have this pattern? I had the next mystery to solve. I designed experiments that attacked this question, but first I had to do field tests to understand the spiral pattern.
I built a test tool to measure the spiral pattern of different species of trees. I took a clear plastic tube and attached two circle protractors that could be rotated up and down the tube. When I put a test branch in the tube, I aligned the zero degree mark on one compass to match up with the first offshoot branch. I then moved and rotated the second compass up to the next branch spot. The second compass measured the angle between the two spots. I recorded the measurement and then moved up the branch step-by-step.
I collected samples of branches that fell to the ground from different trees, and I made measurements. My results confirmed that the Fibonacci sequence was behind the pattern.
But the question of why remained. I knew that branches and leaves collected sunlight for photosynthesis, so my next experiments investigated if the Fibonacci pattern helped. I needed a way to measure and compare the amount of sunlight collected by the pattern. I came up with the idea that I could copy the pattern of branches and leaves with solar panels and compare it with another pattern.

Diagram of tree model that Aidan made with his computer.
I designed and built my own test model, copying the Fibonacci pattern of an oak tree. I studied my results with the compass tool and figured out the branch angles. The pattern was about 137 degrees and the Fibonacci sequence was 2/5. Then I built a model using this pattern from PVC tubing. In place of leaves, I used PV solar panels hooked up in series that produced up to 1/2 volt, so the peak output of the model was 5 volts. The entire design copied the pattern of an oak tree as closely as possible.

Aidan building his solar "tree" collector

The flat-panel collector
I needed to compare the tree design pattern's performance. I made a second model that was based on how man-made solar panel arrays are designed. The second model was a flat-panel array that was mounted at 45 degrees. It had the same type and number of PV solar panels as the tree design, and the same peak voltage. My idea was to track how much sunlight each model collected under the same conditions by watching how much voltage each model made.
I measured the performance of each model with a data logger. This recorded the voltage that each model made over a period of time. The data logger could download the measurements to a computer, and I could see the results in graphs.

The two models collecting sunlight
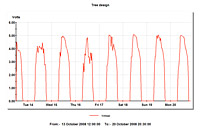
Graph: Tree Design

Graph: Standard Solar

Winter test showing energy collection of the tree and the flat-panel collector

Graph comparing the two solar collector designs

A typical solar collector
I set the two models in the same location in my backyard facing the southern sky and measured their output over a couple of months. I moved the test location around to vary the conditions.
The sunlight conditions were also important. I started my measurements in October and tested my models through December. At that time of year the winter solstice was coming, and the Sun was moving into a lower declination in the sky. The amount of sunshine was shortening. So I was testing the Fibonacci pattern under the most difficult circumstances for collecting sunlight.
I compared my results on graphs, and they were interesting! The Fibonacci tree design performed better than the flat-panel model. The tree design made 20% more electricity and collected 2 1/2 more hours of sunlight during the day. But the most interesting results were in December, when the Sun was at its lowest point in the sky. The tree design made 50% more electricity, and the collection time of sunlight was up to 50% longer!
I had my first evidence that the Fibonacci pattern helped to collect more sunlight. But now I had to go back and figure out why it worked better. I also began to think that I might have found a new way to use nature to make solar panels work better.
I learned that making power from the Sun is not easy. The photovoltaic ("PV") array is the way to do it. A photovoltaic array is a linked collection of multiple solar cells. Making electricity requires as much sunlight as possible. At high noon on a cloudless day at the equator, the power of the Sun is about 1 kilowatt per square meter at the Earth's surface (Komp). Sounds easy to catch some rays, right? But the Sun doesn't stand still. It moves through the sky, and the angle of its rays in regions outside the equator change with the seasons. This makes collecting sunlight tricky for PV arrays. Some PV arrays use tracking systems to keep the panels pointing at the Sun, but these are expensive and need maintenance. So most PV arrays use fixed mounts that face south (or north if you are below the equator).
Fixed mounts have other problems. When a PV array is shaded by another object, like a tree or a house, the solar panels get backed up with electrons like cars in a traffic jam, and the current drops. Dirt, rain, snow and changes in temperature can also hurt electricity production by as much as half! (Komp)
I began to see how nature beat this problem. Collecting sunlight is key to the survival of a tree. Leaves are the solar panels of trees, collecting sunlight for photosynthesis. Collecting the most sunlight is the difference between life and death. Trees in a forest are competing with other trees and plants for sunlight, and even each branch and leaf on a tree are competing with each other for sunlight. Evolution chose the Fibonacci pattern to help trees track the Sun moving in the sky and to collect the most sunlight even in the thickest forest.
I saw patterns that showed that the tree design avoided the problem of shade from other objects. Electricity dropped in the flat-panel array when shade fell on it. But the tree design kept making electricity under the same conditions. The Fibonacci pattern allowed some solar panels to collect sunlight even if others were in shade. Plus I observed that the Fibonacci pattern helped the branches and leaves on a tree to avoid shading each other.
My conclusions suggest that the Fibonacci pattern in trees makes an evolutionary difference. This is probably why the Fibonacci pattern is found in deciduous trees living in higher latitudes. The Fibonacci pattern gives plants like the oak tree a competitive edge while collecting sunlight when the Sun moves through the sky.
My investigation has created more questions to answer. Why are there different Fibonacci patterns among trees? Is one pattern more efficient than another? More testing of other types of trees is needed. I am testing different Fibonacci patterns now. I am improving my tree design model to see if it could be a new way of making panel arrays. My most recent tries with a bigger test model were successful.
The tree design takes up less room than flat-panel arrays and works in spots that don't have a full southern view. It collects more sunlight in winter. Shade and bad weather like snow don't hurt it because the panels are not flat. It even looks nicer because it looks like a tree. A design like this may work better in urban areas where space and direct sunlight can be hard to find.
But the best part of what I learned was that even in the darkest days of winter, nature is still trying to tell us its secrets!
BIBLIOGRAPHY
Adler, I., D. Barabe, and R.V. Jean. "A History of the Study of Phyllotaxis." Annals of Botany 80 (1997): 231-244.
Atela, P., C. Golé, and S. Hotton. "A Dynamical System for Plant Pattern Formation: A Rigorous Analysis." Journal of Nonlinear Science 12.6 (2002): 641-676.
Brockman, C. Frank. Trees of North America: A Guide to Field Identification. New York: Golden Guides from St. Martin's Press, 2001.
Geisel, Theodor Seuss (Dr. Seuss). The Lorax. New York: Random House Publishers, 1971.
Jean, Roger V. Phyllotaxis: A Systematic Study in Plant Morphogenesis. New York: Cambridge University Press, 2009.
Komp, Richard J. Practical Photovoltaics: Electricity from Solar Cells. 3rd. ed. Ann Arbor, Michigan: Aatec Publications, 2001.
Livio, Mario. The Golden Ratio: The Story of Phi, The World's Most Astonishing Number. New York: Broadway Books, 2002.
Posamentier, A., and I. Lehman. The (Fabulous) Fibonacci Numbers. New York: Prometheus Books, 2007.
|
© 2011 American Museum of Natural History. All rights reserved.
|
